Introduction

The Open Compute Stack (OpenCS) framework is a common platform for modelling of problems described by large-scale systems of differential and algebraic equations (ODE or DAE), parallel evaluation of model equations on diverse types of computing devices (including heterogeneous setups), parallel simulation on shared and distributed memory systems, and model exchange.

The framework provides a platform-independent binary interface for model-exchange with the data structures to describe, store in computer memory and evaluate large scale ODE/DAE systems of equations. This approach differs from the typical model-exchange/co-simulation interfaces in that it does not require a human or a machine readable model definition as in modelling and model-exchange languages (i.e. Modelica, gPROMS and CellML) nor a binary interface (C API) implemented in shared libraries (i.e. Simulink and Functional Mock-up Interface).
For instance, in the OpenCS framework model equations are specified in a symbolic form using the OpenCS API, transformed into the bytecode instructions using the operator overloading technique and stored as an array of binary data (a Compute Stack) for direct evaluation by simulators on all platforms/operating systems (including heterogeneous systems) with no additional processing nor compilation steps. Therefore, the same model-specification can be used on any computing platform.
It must be kept in mind that the main purpose is an exchange of individual large-scale models whose equations can be evaluated on different computing devices and which can be simulated on different high-performance computing platforms. Although possible, use of OpenCS models as building blocks for models in other simulators is not the major goal of OpenCS.
Models can contain a coupled set of kernel equations and grouped auxiliary algebraic and differential equations. Each group or kernel can be assigned to a different compute device (processor or accelerator). The framework automatically generates C++ and OpenCL source code for kernels. The source code for C++ shared library kernels is automatically compiled and loaded by the framework.

The OpenCS models can be developed in C++ and Python or exported from simulators using the provided Model Builder API. The structure and the main components of the framework are illustrated in figure below.

API and libraries

The framework includes an API and libraries for:

1. Model specification
   • Direct implementation in C++ and Python
   • Export from simulator-specific data structures
2. Parallel evaluation of model equations
   • The OpenMP API on general purpose processors (multi-core CPUs)
   • The OpenCL framework on streaming processors (GPU, FPGA) and heterogeneous systems (CPU+GPU, CPU+FPGA)
3. Model exchange
   • The models are specified using the OpenCS API and stored as files in a platform-independent binary format (one set of files per processing element)
   • The OpenCS API is used for loading the models into a host simulator and as a common interface to the data required for integration in time by ODE/DAE solvers (i.e. evaluation of equations and derivatives)
4. Simulation on shared memory and distributed memory systems
   • Embedded into a third-party simulator using the OpenCS API
   • Using the standalone ODE/DAE simulator

Use case scenarios

Typical use case scenarios include:

1. Development of custom large-scale models in C++ and Python
2. Parallel evaluation of model equations (i.e. in simulators without a support for parallel evaluation)
3. Universal parallel simulations on shared and distributed memory systems
4. Export of existing models from third-party simulators for model-exchange
5. Use as a simulation engine behind Modelling or Domain Specific Languages
6. Benchmarks between:
   • Simulators
   • ODE/DAE solvers
   • Individual computing devices (i.e. to compare the memory bandwidth and the computation performance)
   • HPC systems
   For example, benchmarks between heterogeneous CPU+GPU and CPU+FPGA systems are possible without re-implementation of the model for multiple diverse architectures: in the OpenCS approach, the identical model-specification is used on all platforms.

The advantages/benefits

The OpenCS framework offers the numerous benefits:

• A single software is used for numerical solution of any system of differential and algebraic equations (ODE or DAE) of any size and on all platforms
• The model specification contains only the low-level model description and therefore can be generated from any modelling software
• The model specification data structures are stored as files in a platform-independent binary format and used as inputs for parallel simulations on all platforms
• Model equations are specified in a platform and programming language independent fashion as an array of binary data (an array of bytecode instructions)
• Equations of any type (differential or algebraic) and any size are supported and can be evaluated on virtually all computing devices (including heterogeneous systems)
• Fast parallel evaluation is achieved using kernels in OpenCL or C++ compiled to machine code
• Each group of equations or kernel can be assigned to a different compute device
• Switching to a different computing device for evaluation of model equations is straightforward and controlled by an input parameter
• For simulations on message-passing systems the partitioning algorithm can utilise multiple balancing constraints to simultaneously balance the memory and computation loads in the critical phases of the numerical solution
• The format of the inter-process communication data is general enough to allow the data exchange to be performed by any communication interface (not only MPI)
• An implementation in standard C99 and C++14 allows compilation for all high-performance computing platforms

The OpenCS methodology

The framework is based on the methodology for parallel numerical solution of general systems of non-linear differential and algebraic equations on shared and distributed memory systems presented in the following articles:

1. Parallelisation of equation-based simulation programs on heterogeneous computing systems (Nikolić, 2018).
2. Parallelisation of equation-based simulation programs on distributed memory systems (Nikolić, 2023a).
3. Open Compute Stack (OpenCS): a framework for parallelisation of equation-based simulation programs (Nikolić, 2023b).
4. Parallelisation of equation-based simulation programs using kernel code generation techniques (Nikolić, 2023c).

The methodology includes the following components:

1. An algorithm for transformation of model equations into a data structure suitable for parallel evaluation on diverse types of computing devices
2. Data structures for model specification that contain all information required for numerical solution such as:
   • the model structure
   • the model equations
   • the sparsity pattern
   • partition data
3. An algorithm for partitioning of general systems of systems using multiple balancing constraints
4. An algorithm for inter-process data exchange
5. The simulation software for integration of general ODE/DAE systems in time

The Key Concepts

Compute Stack	The Reverse Polish (postfix) notation expression stack used as a platform and programming language independent method to describe, store in computer memory and evaluate equations of any type and any size (Nikolić, 2018). Equations can be linear or non-linear, algebraic or differential. Each mathematical operation and its operands are described by a specially designed csComputeStackItem_t data structure, and every equation is transformed into an array of these structures (a Compute Stack).
Compute Stack Machine	A stack machine used to evaluate a single equation (that is a single Compute Stack) using Last In First Out (LIFO) queues.
Compute Stack Evaluator	An interface for parallel evaluation of systems of equations (csComputeStackEvaluator_t class). Evaluators can evaluate either groups of equations or kernels. Two group-evaluator implementations are available (Nikolić, 2018): the OpenMP API is used for parallelisation on general purpose processors the OpenCL framework is used for parallelisation on streaming processors and heterogeneous systems Two kernel-evaluator implementations are available : the OpenMP API is used for parallelisation on general purpose processors the OpenCL framework is used for parallelisation on streaming processors and heterogeneous systems
Compute Stack Model	Data structure that holds the model specification - all information required for the numerical solution, either sequentially or in parallel (csModel_t data structure). For sequential simulations the system is described by a single csModel_t object. For parallel simulations the system is described by an array of csModel_t objects each holding information about one ODE/DAE sub-system. Every model contains the following data: the structure of a model with information about the variable names, types, absolute tolerances and initial conditions: csModelStructure_t structure model equations: csModelEquations_t structure the sparsity pattern of the ODE/DAE (sub-) system (required for evaluation of derivatives): csSparsityPattern_t structure partition data (used for inter-process communication): csPartitionData_t structure
Compute Stack Differential Equations Model	A common interface that provides an API required by ODE/DAE solvers for integration of systems of differential equations in time (csDifferentialEquationModel_t class). It is derived from csModel_t class and provides functions for loading the model from input files, retrieving the sparsity pattern of the ODE/DAE system, setting the variable values/derivatives, exchanging the adjacent variables among the processing elements using the MPI interface, and evaluating equations and derivatives.
Compute Stack Simulator	Software for sequential and parallel simulation of general ODE/DAE systems in time (csSimulator). Simulation inputs are specified in a platform and programming language independent fashion model_structure-[pe].csdata: model variables data model_equations-[pe].csdata: compute stacks and active equation set indexes sparsity_pattern-[pe].csdata: the sparsity pattern partition_data-[pe].csdata: inter-process communication data simulation_options.json: simulation, model, ODE/DAE and linear solver options
Compute Stack Model Builder	A common interface for specification of ODE/DAE Compute Stack models (in C++ and Python). It includes the following functionality: csNumber_t class for specification of model equations. It overloads the standard mathematical functions and operators for creation of Compute Stacks: unary (+, -) and binary (+, -, *, /) mathematical operators, unary (sqrt, log, log10, exp, sin, cos, tan, asin, acos, atan, sinh, cosh, tanh, asinh, acosh, atanh, erf, floor, ceil, and abs) and binary (pow, min, max, atan2) mathematical functions. This way the identical mathematical expressions can be used as in i.e. C/C++. Graph partitioners for partitioning of general systems of equations and load balancing using multiple balancing constraints (Nikolić, 2023a). Export of the developed ODE/DAE models into the input files for sequential/parallel simulations.

Libraries and software provided

The key concepts of the OpenCS framework are implemented in the following libraries:

1. cs_machine.h (header-only Compute Stack Machine implementation in C99)
2. libOpenCS_Evaluators (sequential, OpenMP and OpenCL Compute Stack Evaluator implementations)
3. libOpenCS_Models (Compute Stack Model, Compute Stack Differential Equations Model and Compute Stack Model Builder implementations)
4. libOpenCS_Simulators (ODE and DAE simulators implementations)

and a standalone csSimulator simulator (for both ODE and DAE problems).

Dependencies

The OpenCS framework utilises the following APIs/frameworks:

• OpenMP API
• OpenCL framework
• MPI interface: MPICH on GNU/Linux and macOS, and MS MPI on Windows

and numerical libraries:

• SUNDIALS (CVodes and IDAS)
• Trilinos (AztecOO, IFPACK and ML)
• Boost
• Metis
• HDF5

Background

In general, the model specification for either sequential or parallel simulations are developed using:

• General-purpose programming languages such as C/C++ or Fortran and one of available suites for scientific applications such as SUNDIALS, Trilinos and PETSC
• Modelling languages such as Ascend, APMonitor, gPROMS and Modelica (Dymola, JModelica and OpenModelica)
• Multi-paradigm numerical languages such as Matlab, Scilab, Mathematica and Maple
• Higher-level fourth-generation languages (i.e. Python) such as Assimulo and DAE Tools
• Libraries for Finite Element Analysis (FEA) and Computational Fluid Dynamics (CFD) such as deal.II, libMesh and OpenFOAM
• Computer Aided Engineering (CAE) software for Finite Element Analysis and Computational Fluid Dynamics such as HyperWorks, STAR-CCM+/STAR-CD, COMSOL Multiphysics, ANSYS Fluent/CFX and Abaqus

A detailed discussion of capabilities and limitations of the available approaches for specification of model equations and development of large-scale simulation programs are given in Nikolić (2016, 2018, 2023a and 2023b).

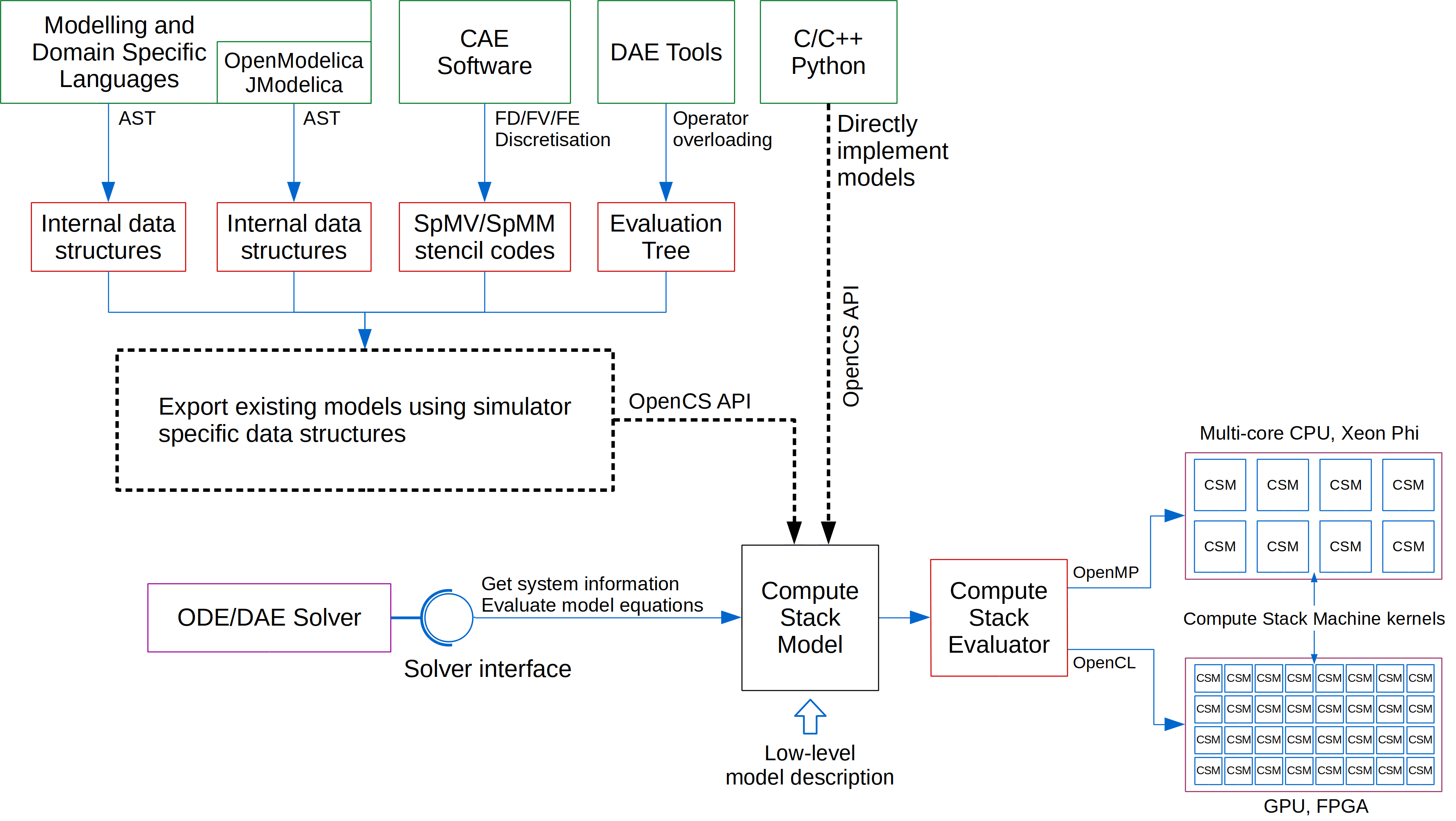
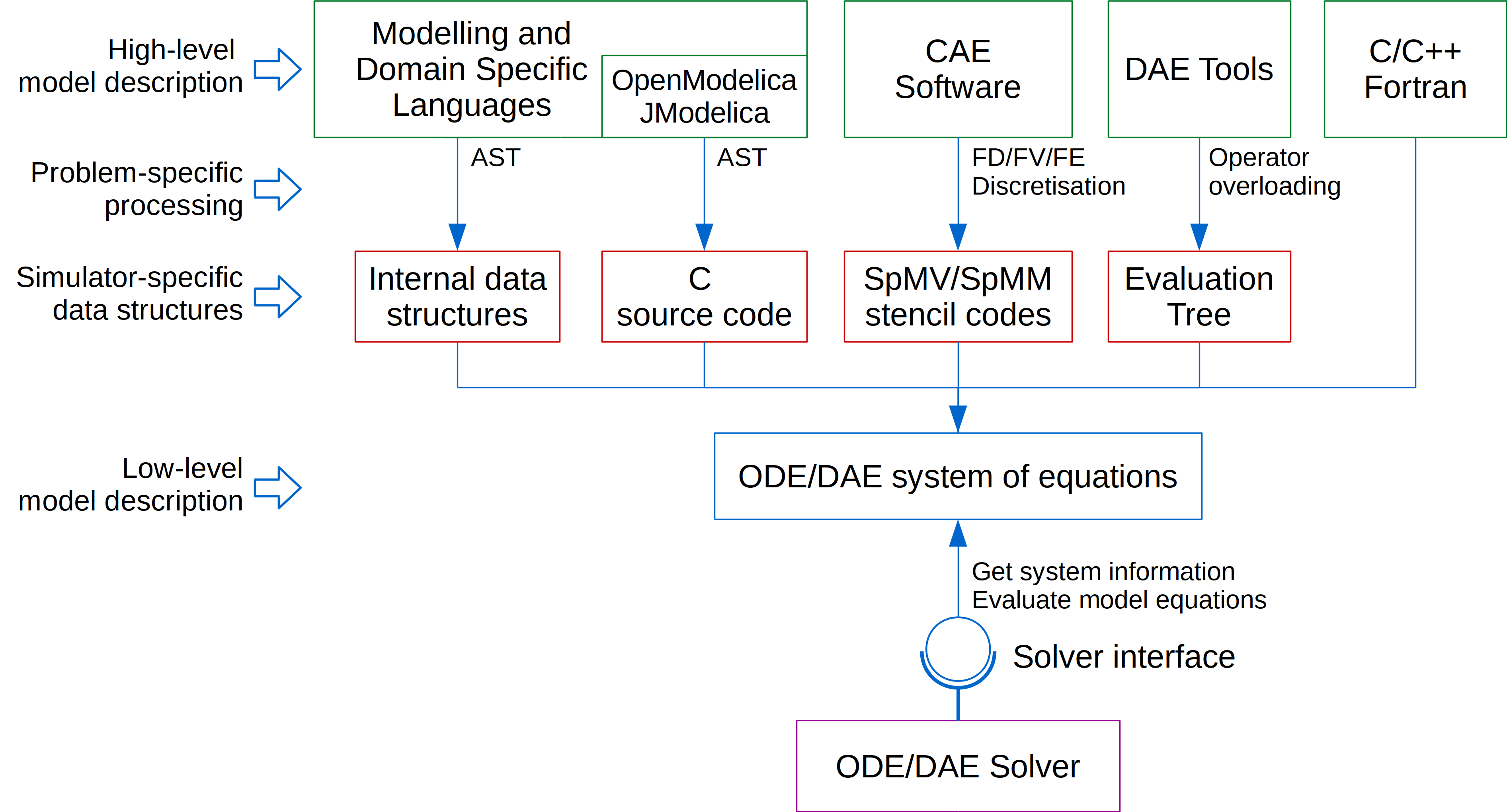
In all approaches, an interface to a particular ODE/DAE solver must be implemented to provide the information required for numerical integration in time. The solver interface is directly implemented in general-purpose programming languages (i.e. as user-supplied functions). In other approaches, the solver interface is built around the internal simulator-specific data structures representing the model. For instance, the source code of modelling languages is typically parsed into an Abstract Syntax Tree (AST). The produced AST can be transformed into a simulator-specific data structure or used to generate C source code as in OpenModelica and JModelica. Other modelling software such as DAE Tools use the operator overloading technique to produce a tree-like data structure (Evaluation Tree). CAE software perform a discretisation of Partial Differential Equations (PDE) on a specified grid: (a) on unstructured grids, the results of discretisation using the Finite Element (FE) or Finite Volume (FV) methods are the mass and stiffness matrices and load vectors, and (b) on structured grids, the results of discretisation using the Finite Difference (FD) method are the stencil data (nodes arrangement and their coefficients). The simulator-specific data structures, sparse matrix-vector (SpMV) and matrix-matrix (SpMM) operations or stencil codes are then utilised by the ODE/DAE solver interface to evaluate model equations and derivatives.

The main idea in the OpenCS approach is to separate a high-level (simulator-dependent) model specification procedure, typically performed only once, from its parallel (in general, simulator-independent) numerical solution. While description of models and generation of a system of equations can be performed in many different ways depending on the type of the problem and the method applied by a simulator, the numerical solution procedure always requires the same (low-level) information. For instance, a high-level model specification for the problems governed by partial differential equations can be created using a modelling language or a CAE software. The low-level model description is internally generated by simulators utilising various discretisation methods and results in a system of differential equations (ODE or DAE). However, the information required for numerical solution in both cases are essentially identical: the data about the number of variables, their names, types, absolute tolerances and initial conditions, and the functions for evaluation of equations and derivatives. Therefore, the low-level model description coupled with a method for parallel evaluation of model equations on different computing devices can be a basis for a universal software for parallel simulation of general systems of differential equations on all important platforms. In general, such a model description, due to its simplicity, can be generated and utilised by any existing simulator. This way, simulations can be performed on platforms not supported by that particular simulator or the simulation performance on the supported platforms can be improved by evaluating model equations in parallel on devices that are not currently utilised. In addition, the same platform-independent model description can be used for model exchange and benchmarks between different simulators, solvers, individual computing devices and high performance computing platforms (i.e. between heterogeneous clusters, where evaluation of model equations is currently not available for different architectures). An efficient evaluation of model equations is of utmost importance. For instance, very often more than 85% of the total integration time is spent on evaluation of equations and derivatives (Nikolic, 2018). Since most of the modern computers and many specially designed clusters are equipped with additional stream processors/accelerators such as Graphics Processing Units (GPU) and Field Programmable Gate Arrays (FPGA), the simulation software must be specially designed to effectively take advantage of multiple architectures. While parallel evaluation of model equations on general purpose processors is fairly straightforward and different techniques are applied by different simulators, evaluation on streaming processors is rather difficult. Stream computing differs from traditional computing in that the system processes a sequential stream of elements: a kernel is executed on each element of the input stream and the result stored in an output stream. Thus, the data structures representing the model equations must be designed to support evaluation on both systems (often simultaneously in heterogeneous computing setups).

To this end, the Open Compute Stack (OpenCS) framework has been develop to provide:

1. Model specification data structures for a platform-independent description of general ODE/DAE systems of equations
2. A platform-independent method to describe, store in computer memory and evaluate general systems of equations of any size on diverse types of computing devices
3. An Application Programming Interface (API) for model specification, parallel evaluation of model equations, model exchange and a generic interface to ODE/DAE solvers
4. Algorithms for partitioning of general systems of equations and inter-process data exchange (for simulations on distributed memory systems)
5. Simulation software for parallel numerical solution of general ODE/DAE systems of equations on shared and distributed memory systems

This way, the OpenCS framework offers a common platform for specification of equation-based models, parallel evaluation of equations on diverse types of computing devices, model exchange and parallel simulation of large-scale systems of differential equations on shared and distributed memory systems.

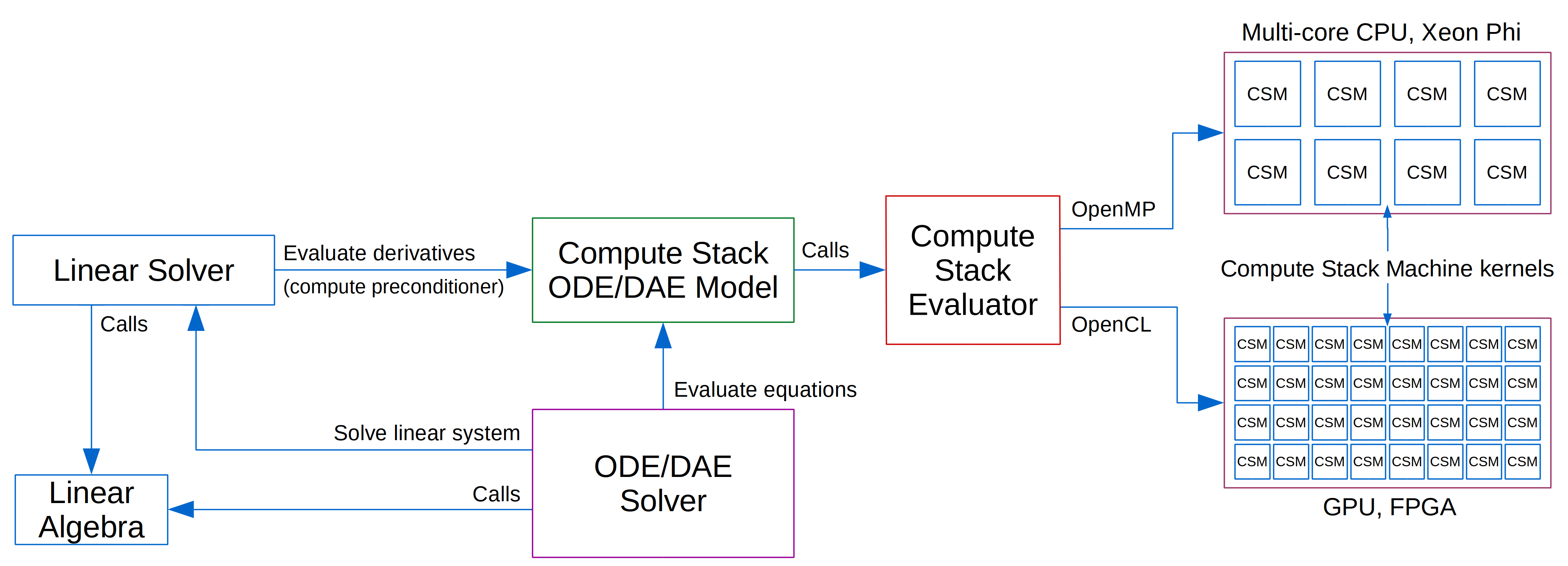
On shared memory systems simulations are executed on a single processing element utilising the available computing hardware (i.e. multi-core CPU, GPU or heterogeneous CPU+GPU):

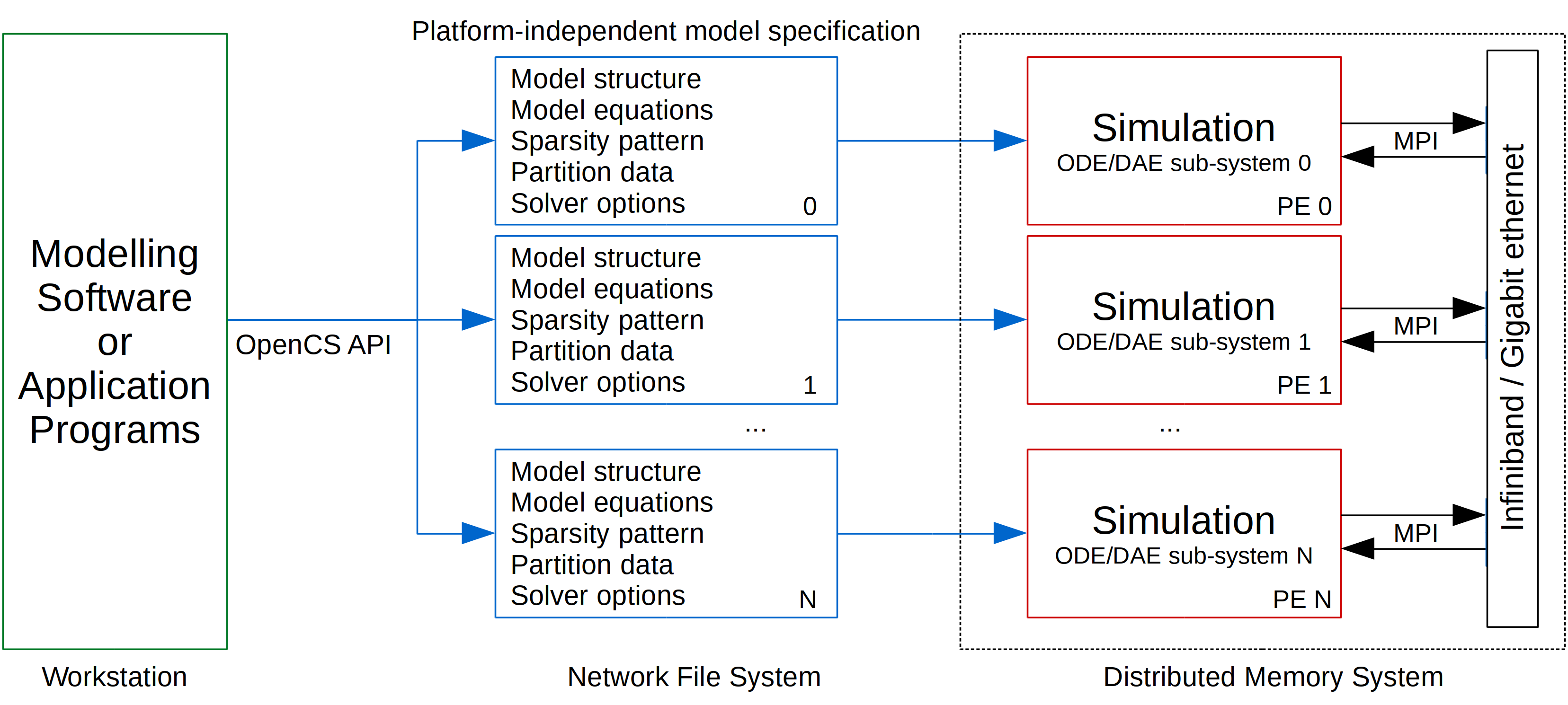
On distributed memory systems simulations are executed on a number of processing elements where every processing element integrates one part (sub-system) of the overall ODE/DAE system in time and performs an inter-process communication to exchange the data between processing elements:

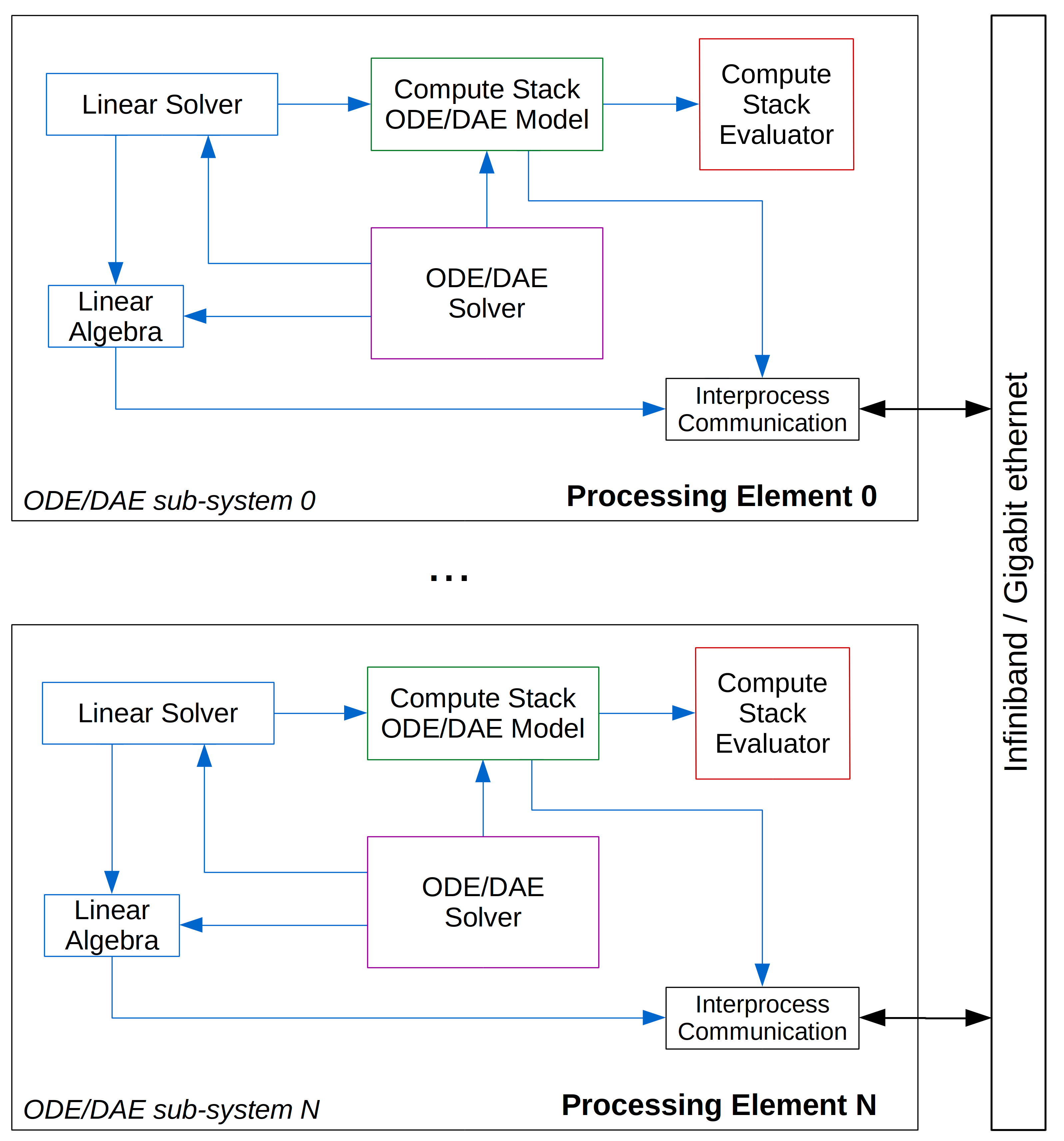
Simulation inputs are specified in a generic fashion as files in a (platform independent) binary format. The input files are generated by a modelling software (i.e. DAE Tools) and contain the serialised model specification data structures and solver options. In addition, streaming processors/accelerators available on individual processing elements such as General Purpose Graphics Processing Units (GPGPU) and Field Programmable Gate Arrays (FPGA) can be utilised for evaluation of model equations (Nikolić, 2018). The input data files are generated for one or more processing elements and stored in a local or a Network File System.

The OpenCS models can be developed in C++ and Python or exported from simulators using the provided Model Builder API.